Examples¶
Refractive index and radius determination¶
OPD edge-detection approach with a single cell¶
This example illustrates how qpsphere can be used to determine
the radius and the refractive index of a spherical cell.
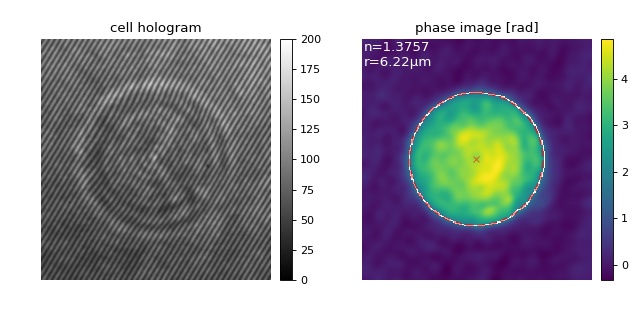
The hologram of the myeloid leukemia cell (HL60) on the left was
recorded using digital holographic microscopy (DHM).
In the quantitative phase image on the right, the detected cell
contour (white) and the subsequent circle fit (red) as well as the
resulting average radius and refractive index of the cell
are shown. The setup used for recording these data is described in
[Schuermann2015] which also contains a description of the
basic steps to determine the position and radius of the cell and
to subsequently compute the average refractive index from the
experimental phase data. The experimental data is loaded and
background-corrected using qpimage.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 | import matplotlib
import matplotlib.pylab as plt
import numpy as np
import qpimage
import qpsphere
# load the experimental data
edata = np.load("./data/hologram_cell.npz")
# create QPImage instance
qpi = qpimage.QPImage(data=edata["data"],
bg_data=edata["bg_data"],
which_data="hologram",
meta_data={"wavelength": 633e-9,
"pixel size": 0.107e-6,
"medium index": 1.335
}
)
# background correction
qpi.compute_bg(which_data=["amplitude", "phase"],
fit_offset="fit",
fit_profile="tilt",
border_px=5,
)
# determine radius and refractive index, guess the cell radius: 10µm
n, r, (cx, cy), edge = qpsphere.edgefit.analyze(qpi=qpi,
r0=10e-6,
ret_center=True,
ret_edge=True)
# plot results
fig = plt.figure(figsize=(8, 4))
matplotlib.rcParams["image.interpolation"] = "bicubic"
holkw = {"cmap": "gray",
"vmin": 0,
"vmax": 200}
# hologram image
ax1 = plt.subplot(121, title="cell hologram")
map1 = ax1.imshow(edata["data"].T, **holkw)
plt.colorbar(map1, ax=ax1, fraction=.048, pad=0.04)
# phase image
ax2 = plt.subplot(122, title="phase image [rad]")
map2 = ax2.imshow(qpi.pha.T)
# edge
edgeplot = np.ma.masked_where(edge == 0, edge)
ax2.imshow(edgeplot.T, cmap="gray_r", interpolation="none")
# fitted circle center
plt.plot(cx, cy, "xr", alpha=.5)
# fitted circle perimeter
circle = plt.Circle((cx, cy), r / qpi["pixel size"],
color='r', fill=False, ls="dashed", lw=2, alpha=.5)
ax2.add_artist(circle)
# fitting results as text
info = "n={:.4F}\nr={:.2f}µm".format(n, r * 1e6)
ax2.text(.8, .8, info, color="w", fontsize="12", verticalalignment="top")
plt.colorbar(map2, ax=ax2, fraction=.048, pad=0.04)
# disable axes
[ax.axis("off") for ax in [ax1, ax2]]
plt.tight_layout()
plt.show()
|
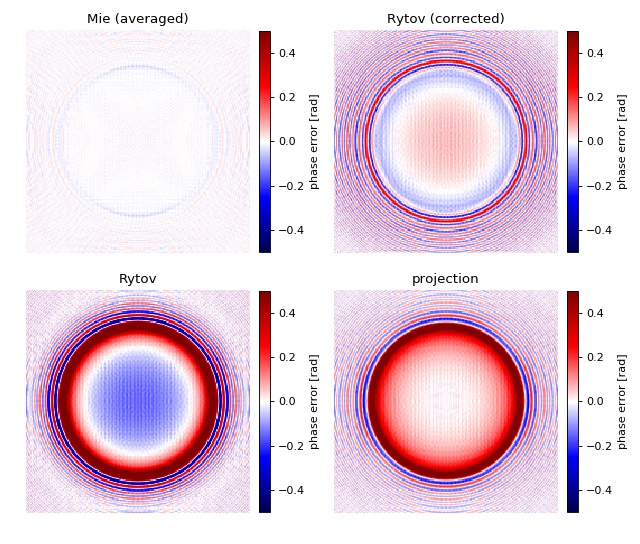
Comparison of light-scattering models¶
The phase error map allows a comparison of the ability of the modeling methods implemented in qpsphere to reproduce the phase delay introduced by a dielectric sphere. For a quantitative comparison, see reference [Mueller2018].
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 | import matplotlib.pylab as plt
import qpsphere
kwargs = {"radius": 10e-6, # 10µm
"sphere_index": 1.380, # cell
"medium_index": 1.335, # PBS
"wavelength": 647.1e-9, # krypton laser
"grid_size": (200, 200),
}
px_size = 3 * kwargs["radius"] / kwargs["grid_size"][0]
kwargs["pixel_size"] = px_size
# mie (long computation time)
qpi_mie = qpsphere.simulate(model="mie", **kwargs)
# mie averaged
qpi_mie_avg = qpsphere.simulate(model="mie-avg", **kwargs)
# rytov corrected
qpi_ryt_sc = qpsphere.simulate(model="rytov-sc", **kwargs)
# rytov
qpi_ryt = qpsphere.simulate(model="rytov", **kwargs)
# projection
qpi_proj = qpsphere.simulate(model="projection", **kwargs)
kwargs = {"vmin": -.5,
"vmax": .5,
"cmap": "seismic"}
plt.figure(figsize=(8, 6.8))
ax1 = plt.subplot(221, title="Mie (averaged)")
pmap = plt.imshow(qpi_mie.pha - qpi_mie_avg.pha, **kwargs)
ax2 = plt.subplot(222, title="Rytov (corrected)")
plt.imshow(qpi_mie.pha - qpi_ryt_sc.pha, **kwargs)
ax3 = plt.subplot(223, title="Rytov")
plt.imshow(qpi_mie.pha - qpi_ryt.pha, **kwargs)
ax4 = plt.subplot(224, title="projection")
plt.imshow(qpi_mie.pha - qpi_proj.pha, **kwargs)
# disable axes
for ax in [ax1, ax2, ax3, ax4]:
ax.axis("off")
plt.colorbar(pmap, ax=ax, fraction=.045, pad=0.04,
label="phase error [rad]")
plt.tight_layout(w_pad=0, h_pad=0)
plt.show()
|
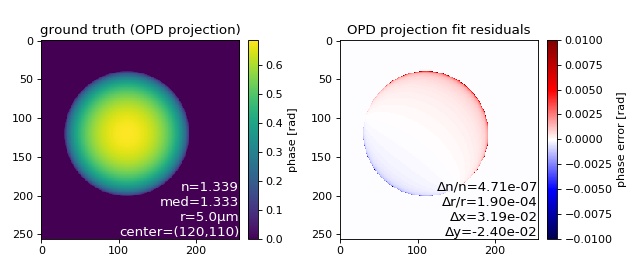
OPD projection image fit applied to an OPD simulation¶
This examples illustrates how the refractive index and radius of a sphere can be determined using the 2D (image-based) phase fitting algorithm.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 | import matplotlib.pylab as plt
import qpsphere
# run simulation with projection model
r = 5e-6
n = 1.339
med = 1.333
c = (120, 110)
qpi = qpsphere.simulate(radius=r,
sphere_index=n,
medium_index=med,
wavelength=550e-9,
grid_size=(256, 256),
model="projection",
center=c)
# fit simulation with projection model
n_fit, r_fit, c_fit, qpi_fit = qpsphere.analyze(qpi=qpi,
r0=4e-6,
method="image",
model="projection",
imagekw={"verbose": 1},
ret_center=True,
ret_qpi=True)
# plot results
fig = plt.figure(figsize=(8, 3.5))
txtkwargs = {"verticalalignment": "bottom",
"horizontalalignment": "right",
"fontsize": 12}
ax1 = plt.subplot(121, title="ground truth (OPD projection)")
map1 = ax1.imshow(qpi.pha)
plt.colorbar(map1, ax=ax1, fraction=.046, pad=0.04, label="phase [rad]")
t1 = "n={:.3f}\nmed={:.3f}\nr={:.1f}µm\ncenter=({:d},{:d})".format(
n, med, r * 1e6, c[0], c[1])
ax1.text(1, 0, t1, transform=ax1.transAxes, color="w", **txtkwargs)
ax2 = plt.subplot(122, title="OPD projection fit residuals")
map2 = ax2.imshow(qpi.pha - qpi_fit.pha, vmin=-.01, vmax=.01, cmap="seismic")
plt.colorbar(map2, ax=ax2, fraction=.046, pad=0.04, label="phase error [rad]")
t2 = "Δn/n={:.2e}\nΔr/r={:.2e}\nΔx={:.2e}\nΔy={:.2e}".format(
abs(n - n_fit) / n, abs(r - r_fit) / r,
c_fit[0] - c[0], c_fit[1] - c[1])
ax2.text(1, 0, t2, transform=ax2.transAxes, color="k", **txtkwargs)
plt.tight_layout()
plt.show()
|
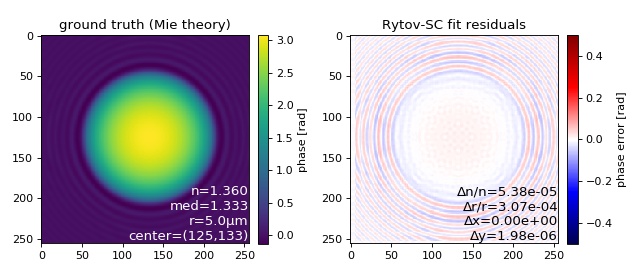
Rytov-SC image fit applied to a Mie simulation¶
This examples illustrates how the refractive index and radius of a sphere can be determined accurately using the 2D phase fitting algorithm with the systematically corrected Rytov approximation.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 | import matplotlib.pylab as plt
import qpsphere
# run simulation with averaged Mie model
r = 5e-6
n = 1.360
med = 1.333
c = (125, 133)
qpi = qpsphere.simulate(radius=r,
sphere_index=n,
medium_index=med,
wavelength=550e-9,
grid_size=(256, 256),
model="mie-avg",
center=c)
# Fitting Mie simulations with the systematically corrected Rytov
# approximation (`model="rytov sc"`) yields lower parameter errors
# compared to the non-corrected Rytov approximation (`model="rytov"`).
n_fit, r_fit, c_fit, qpi_fit = qpsphere.analyze(qpi=qpi,
r0=4e-6,
method="image",
model="rytov-sc",
imagekw={"verbose": 1},
ret_center=True,
ret_qpi=True)
# plot results
fig = plt.figure(figsize=(8, 3.5))
txtkwargs = {"verticalalignment": "bottom",
"horizontalalignment": "right",
"fontsize": 12}
ax1 = plt.subplot(121, title="ground truth (Mie theory)")
map1 = ax1.imshow(qpi.pha)
plt.colorbar(map1, ax=ax1, fraction=.046, pad=0.04, label="phase [rad]")
t1 = "n={:.3f}\nmed={:.3f}\nr={:.1f}µm\ncenter=({:d},{:d})".format(
n, med, r * 1e6, c[0], c[1])
ax1.text(1, 0, t1, transform=ax1.transAxes, color="w", **txtkwargs)
ax2 = plt.subplot(122, title="Rytov-SC fit residuals")
map2 = ax2.imshow(qpi.pha - qpi_fit.pha, vmin=-.5, vmax=.5, cmap="seismic")
plt.colorbar(map2, ax=ax2, fraction=.046, pad=0.04, label="phase error [rad]")
t2 = "Δn/n={:.2e}\nΔr/r={:.2e}\nΔx={:.2e}\nΔy={:.2e}".format(
abs(n - n_fit) / n, abs(r - r_fit) / r,
c_fit[0] - c[0], c_fit[1] - c[1])
ax2.text(1, 0, t2, transform=ax2.transAxes, color="k", **txtkwargs)
plt.tight_layout()
plt.show()
|
Other examples¶
- Background correction based
on the mask image determined with the convenience method
qpsphere.cnvnc.bg_phase_mask_for_qpi().